تست 11 (سال 77)
مجموعه ی نقاط مرزی یک مجموعه ی E از یک فضای متریک، مجموعه ای است ...
1) باز
2) بسته
3) هم باز و هم بسته
4) نه باز و نه بسته
حل تست:
گزینه ی 2.
مرز زیر فضای E از X، مجموعه ی نقاطی از فضای X است که هر همسایگی از هر نقطه ی آن، اشتراکی ناتهی با E و متمم E داشته باشد. با کمی دقت می توان ثابت کرد که متمم مرز، باز و در نتیجه مرز، مجموعه ای بسته است. (البته راه دیگر، اثبات این مطلب است که مرز E، شامل نقاط حدی خود است.)
هر گاه X یک فضای متریک، 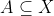 فشره و
فشره و 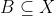 باز باشد، آنگاه ........... فشرده است.
باز باشد، آنگاه ........... فشرده است.
1) 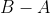
2) 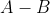
3) 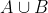
4) 
حل تست:
گزینه ی 2.
می نوان نوشت: 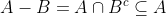 ؛ چون
؛ چون 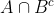 بسته و زیر مجموعه ای از یک فضای فشرده است، بنابر خودش نیز یک فضای فشرده است.
بسته و زیر مجموعه ای از یک فضای فشرده است، بنابر خودش نیز یک فضای فشرده است.
تست 13 (سال 78)
هرگاه 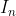 دنباله ی آشیانی از فواصل غیر تهی در
دنباله ی آشیانی از فواصل غیر تهی در 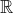 باشد، تحت کدام یک از شرایط زیر،
باشد، تحت کدام یک از شرایط زیر، 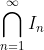 ناتهی است؟
ناتهی است؟
1) 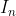 ها بسته باشند.
ها بسته باشند.
2) 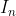 ها بسته و کراندار باشند.
ها بسته و کراندار باشند.
3) 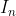 ها کراندار باشند.
ها کراندار باشند.
4) 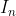 ها همبند باشند.
ها همبند باشند.
حل تست:
گزینه ی 2.
شرط اصلی، فشرده بودن است؛ اما در 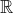 فشردگی معادل بسته و کراندار است.
فشردگی معادل بسته و کراندار است.
تست 14 (سال 78)
اگر A و B زیر مجموعه های 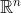 باشند، به قسمی که A بسته و B فشرده باشد و
باشند، به قسمی که A بسته و B فشرده باشد و 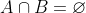 ، در این صورت کدام گزینه صحیح نمی باشد؟
، در این صورت کدام گزینه صحیح نمی باشد؟
1) A+B بسته است.
2) مجموعه ی بازی مانند V شامل A وجود دارد، به قسمی که 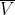 فشرده و
فشرده و 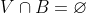 .
.
3) تابع پیوسته ای مانند 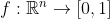 وجود دارد به قسمی که
وجود دارد به قسمی که 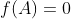 و
و 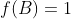 .
.
4) نقاطی مانند 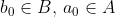 وجود دارند به قسمی که
وجود دارند به قسمی که
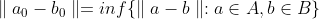
حل تست:
گزینه ی 2.
اگر A بی کران باشد، 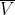 نیز بی کران است و نمی تواند فشرده باشد.
نیز بی کران است و نمی تواند فشرده باشد.
تست 15 (سال 78)
اگر 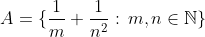 ، در این صورت بستار
، در این صورت بستار 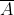 (کوچکترین مجموعه ی بسته در
(کوچکترین مجموعه ی بسته در 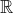 و شامل A) عبارت است از:
و شامل A) عبارت است از:
1) 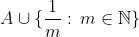
2) 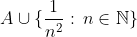
3) 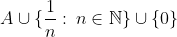
4) 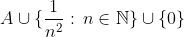
حل تست:
گزینه ی 3.
m را ثابت نگاه دارید و n را به بی نهایت میل دهید؛ هم چنین n و m را با هم به بی نهایت میل دهید. ثابت کنید A غیر از این ها نقطه ی حدی دیگری ندارد.
تست 16 (سال 79)
اگر 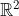 با متر معمولی در نظر گرفته شود، مجموعه ی
با متر معمولی در نظر گرفته شود، مجموعه ی 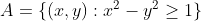 مجموعه ای است ..........
مجموعه ای است ..........
1) فشرده و همبند
2) نه فشرده و نه همبند
3) فشرده و ناهمبند
4) همبند است ولی فشرده نیست.
حل تست:
گزینه ی 2.
شکل A داخل هذلولی همراه با مرزهای آن است، بنابر این بی کران است و در نتیجه فشرده نیست؛ هم چنین به وضوح همبند نیست.
در فضای متریک 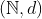 که
که 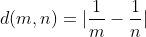 ، مجموعه ی
، مجموعه ی 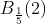 (یعنی گوی باز به مرکز 2 و شعاع یک پنجم) برابر است با:
(یعنی گوی باز به مرکز 2 و شعاع یک پنجم) برابر است با:
1) 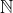
2) 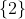
3) 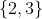
4) 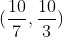
حل تست:
گزینه ی 4.
کافی است تعریف گوی باز را بنویسید.
تست 18 (سال 80)
اگر 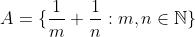 ، آنگاه
، آنگاه  کدام است؟
کدام است؟
1) 
2) 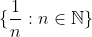
3) 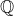
4) 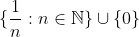
حل تست:
گزینه ی 1.
A یک زیر فضای گسسته ی یک فضای متری اقلیدسی ناشماراست و لذا A شامل هیچ همسایگی از نقاط خود نیست.
تست 19 (سال 80)
قرار دهید 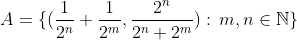 به عنوان زیر مجموعه ای از زوجهای مرتب در
به عنوان زیر مجموعه ای از زوجهای مرتب در 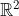 .
.
1) 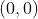 نقطه ی درونی A است.
نقطه ی درونی A است.
2) مجموعه ی A باز است.
3) مجموعه ی A بسته است.
4) 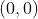 نقطه ی حدی این مجموعه است.
نقطه ی حدی این مجموعه است.
حل تست:
گزینه ی 4.
اگر یک بار m را ثابت نگاه دارید و n را به بی نهایت میل دهید و سپس m را به بی نهایت میل دهید، مشخص است که مبدأ نقطه ی حدی A است که عضو آن نیست. پس 3 درست نیست. از طرفی A شماراست و لذا 1 و 2 درست نیست.
ست 20 (سال 80)
کدام گزینه نادرست است؟
1) اجتماع هر دو مجموعه همبند با اشتراک ناتهی مجموعه ای است همبند.
2) اشتراک هر دو مجموعه ی همبند 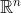 برای
برای 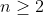 ، مجموعه ای است همبند.
، مجموعه ای است همبند.
3) تنها زیر مجموعه ی (ناتهی) همبند فضای اعداد گویا، تک عنصری است.
4) تنها زیر مجموعه های (ناتهی) همبند فضای متریک گسسته، تک عنصری هستند.
حل تست:
گزینه ی 1.
دو قرص بسته ی مماس بر هم را در نظر بگیرید. هریک از آنها همبند ولی اجتماع آن ها همبند نیست.
نکته: برای گزینه ی 4 به اینجا مراجعه کنید. (یك فضای گسسته همبند نیست مگر اینكه تك عضوی باشد. زیرا در غیر این صورت مجموعه همه ی تك عضویها تشكیل یك جداسازی برای این فضا می دهد(چون در فضای گسسته هر مجموعه ی تك عضوی هم باز است وهم بسته) و می دانیم كه هر فضایی كه دارای یك جداسازی باشد همبند نیست. پس هر فضای گسسته با بیش از یك عضو همبند نیست.)
تست 21 (سال 80)
در فضای متریک 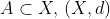 ، کدام عبارت، مرز مجموعه ی A نیست؟
، کدام عبارت، مرز مجموعه ی A نیست؟
1) 
2) 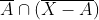
3) 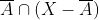
4) 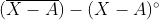
حل تست:
گزینه ی 3.
با توجه به تعریف، مرز 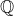 عبارت است از
عبارت است از 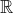 ؛ حال کافی است قرار دهید
؛ حال کافی است قرار دهید 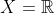 و
و 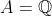 .
.
تست 22 (سال 81)
فرض کنید 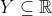 و
و 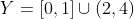 ؛ آنگاه
؛ آنگاه
1) 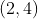 فشرده در Y است.
فشرده در Y است.
2) 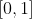 باز و بسته در Y است.
باز و بسته در Y است.
3) 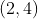 کامل در Y است.
کامل در Y است.
4) 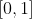 چگال در Y است.
چگال در Y است.
حل تست:
گزینه ی 2 و 3 !!
به وضوح هر نقطه ی 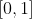 ، نقطه ی داخلی (نسبت به متر Y) است و
، نقطه ی داخلی (نسبت به متر Y) است و 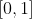 شامل نقاط حدی خود است؛ همچنین
شامل نقاط حدی خود است؛ همچنین 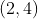 مساوی نقاط حدی خود (البته به عنوان زیر فضای Y) و لذا کامل است.
مساوی نقاط حدی خود (البته به عنوان زیر فضای Y) و لذا کامل است.
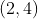 در Y فشرده نیست، زیرا در
در Y فشرده نیست، زیرا در 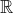 فشرده نیست.
فشرده نیست. 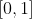 چگال در Y نیست، زیرا با بستار خود مساوی است.
چگال در Y نیست، زیرا با بستار خود مساوی است.
تست 23 (سال 81)
کدام یک از نقاط، انباشتگی (تجمع یا حدی) مجموعه ی 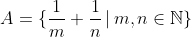 است؟
است؟
1) 
2) 1
3) 
4) 2
حل تست:
گزینه ی 2.
قرار دهید m=1 و n را به بی نهایت میل دهید. (نقاط انباشتگی A مجموعه ی 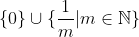 است.)
است.)
کدام یک از توابع d در اعداد حقیقی، متر نیست؟
1) 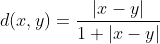
2) 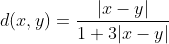
3) 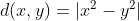
4) 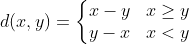
حل تست:
گزینه ی 3.
در گزینه ی 3 داریم: 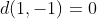 که مخالف تعریف متر است.
که مخالف تعریف متر است.
تست 25 (سال 81)
فرض کنید 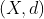 یک فضای متریک و
یک فضای متریک و 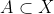 ؛ کدام گزینه همواره درست است؟
؛ کدام گزینه همواره درست است؟
1) اگر A همبند نامتناهی باشد، آنگاه 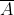 کامل (Perfect) است.
کامل (Perfect) است.
2) اگر A کامل و کراندار باشد، آنگاه A فشرده است.
3) اگر A کامل باشد، آنگاه A ناشماراست.
3) اگر A کامل باشد، آنگاه همبند است.
حل تست:
گزینه ی 1.
برای اثبات گزینه ی 1، ثابت کنید که اگر 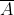 کامل نباشد، عضوی از A مانند a که نقطه ی تنهای آن است وجود دارد به گونه ای که مجموعه ی
کامل نباشد، عضوی از A مانند a که نقطه ی تنهای آن است وجود دارد به گونه ای که مجموعه ی 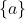 در A هم باز است و هم بسته که متناقض همبندی A است. برای رد سه گزینه ی دیگر، X را اعداد گویا و A را مجموعه ی همه ی اعداد گویا در بازه ی
در A هم باز است و هم بسته که متناقض همبندی A است. برای رد سه گزینه ی دیگر، X را اعداد گویا و A را مجموعه ی همه ی اعداد گویا در بازه ی 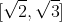 فرض کنید.
فرض کنید.







